Step-by-step explanation
How to know that x=4 is not a solution to an equation? To verify this, we just evaluate the equation for x=4, to obtain a contradiction.
Let's do this for the first equation:
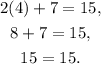
Here, we didn't get a contradiction (15 is equal to itself). This means that x=4 is indeed a solution to this equation.
Let's test the second one:
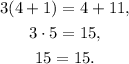
As before, we have that x=4 is a solution.
Let's test the third one:
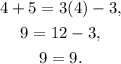
Again, x=4 is a solution.
Finally, let's verify the last one:
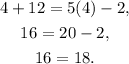
We got a contradiction! 16 is not equal to 18.
Answer
The answer is the fourth option (equation).