To answer this question, we must noted that:
The slopes of two perpendicular lines are negative reciprocals of each other:
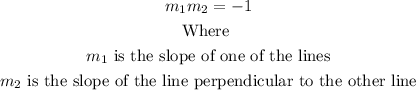
First, we will find what the slope of the initial equation is:
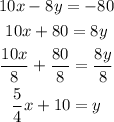
So from the above solution, we see that:
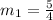
We will solve for the slope of a line perpendicular to it thus:
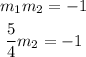
Simplifying further:
