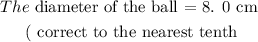SOLUTION:
Step 1:
In this question, we are given the following:
A ball has a volume of 86π cubic centimeters.
What is the diameter of the ball? Show all work and round to the nearest tenth.
Step 2:
The details of the solution are as follows:
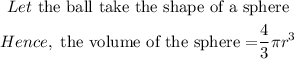
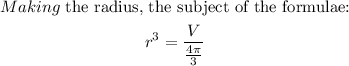
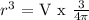
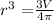
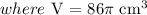
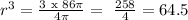
![\begin{gathered} r\text{ =}\sqrt[3]{64.\text{ 5}} \\ \text{r = 4.010 cm} \\ Then\text{ the diameter = 2 x 4.010 cm = 8.02 cm }\approx\text{ 8. 0 cm } \\ \text{\lparen correct to the nearest tenth \rparen} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v67lx128fvupy8xu51teqt7cqk1z4is3ai.png)
CONCLUSION:
The final answer is: