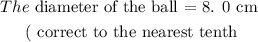Question

A ball has a volume of 86π cubic centimeters. What is the diameter of the ball? Show all work and round to the nearest tenth.

Answer 1

Step 1:

In this question, we are given the following:

A ball has a volume of 86π cubic centimeters.

What is the diameter of the ball? Show all work and round to the nearest tenth.

Step 2:

The details of the solution are as follows:

`\begin{gathered} Let\text{ the ball take the shape of a sphere} \\ Hence,\text{ the volume of the sphere =}(4)/(3)\pi r^3 \end{gathered}`
`\begin{gathered} Making\text{ the radius, the subject of the formulae:} \\ r^3=(V)/((4\pi)/(3)) \end{gathered}`
`r^3\text{ = V x }(3)/(4\pi)`
`r^3\text{ =}(3V)/(4\pi)`
`where\text{ V = 86}\pi\text{ cm}^3`
`r^3=\frac{3\text{ x 86}\pi}{4\pi}=\text{ }(258)/(4)=64.5`
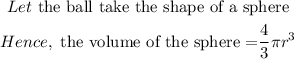
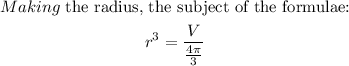
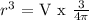
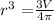
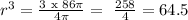
`\begin{gathered} r\text{ =}\sqrt[3]{64.\text{ 5}} \\ \text{r = 4.010 cm} \\ Then\text{ the diameter = 2 x 4.010 cm = 8.02 cm }\approx\text{ 8. 0 cm } \\ \text{\lparen correct to the nearest tenth \rparen} \end{gathered}`

CONCLUSION:

The final answer is:

`\begin{gathered} The\text{ diameter of the ball = 8. 0 cm } \\ (\text{ correct to the nearest tenth\rparen} \end{gathered}`