Question

Determine from the given points of two lines if the lines are parallel, perpendicular, or neither. Line a: (-3, 1) and (-7, -2)Line b: (2, -1) and (8, 4)What is the slope of line a?What is the slope of line b?Are the slopes the same?Are the slopes opposite recipricals?Are the lines perpendicular, parallel, or neither?

Answer 1

• Slope of line a: 3/4

,

• Slope of line b: 5/6

,

• The lines are ,neither parallel nor perpendicular

Step-by-step explanation

The slope of a line that passes through points (x₁, y₁) and (x₂, y₂) is,

`m=(y_1-y_2)/(x_1-x_2)`

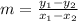
Line a passes through the points (-3, 1) and (-7, -2). Its slope is,

`m_a=(1-(-2))/(-3-(-7))=(1+2)/(-3+7)=(3)/(4)`

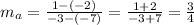
Line b passes through the points (2, -1) and (8, 4). Its slope is,

`m_b=(-1-4)/(2-8)=(-5)/(-6)=(5)/(6)`

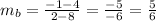
Two lines are parallel if they have the same slope, and they are perpendicular if they have opposite reciprocal slopes.

In this case, the slopes of lines a and b are different, so they are not parallel. They are not opposite reciprocal either, so they are not perpendicular. Hence, the lines are neither parallel nor perpendicular.