a) The total cost can be expressed as the sum of a fixed cost, which is the initial cost of $350, and a variable cost, which is $5 per lawn.
Then, we can write the total cost C(x) as:
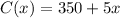
b) We know that the profit function is P(x) = 9x - 350.
We have to find the revenue function R(x).
We know that the profit function P(x) is equal to the revenue R(x) minus the cost C(x), so we can write:
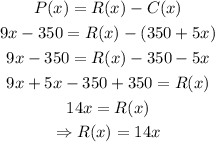
c) We see from the revenue function R(x) = 14x that he charges $14 per lawn.
We can calculate how many lawns (x) he has to mow in order to make a profit.
This can be calculated as the x that makes P(x) = 0:
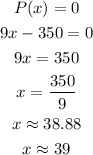
He will make a profit after mowing 39 lawns.
Answer: a) the total cost is C(x) = 350 + 5x.
b) the revenue function is R(x) = 14x.
c) he charges $14 per lawn. He need