Question

a) What is the pressure drop (in N/m2) due to the Bernoulli effect as water goes into a 3.10 cm diameter nozzle from a 9.20 cm diameter fire hose while carrying a flow of 38.0 L/s? N/m2(b) To what maximum height (in m) above the nozzle can this water rise? (The actual height will be significantly smaller due to air resistance.) m

Answer 1

Given:

Diameter of noxxle = 3.10 cm

Diameter of hose = 9.20 cm

Flow = 38.0 L/s

Let's solve for the following:

(a). Let's find the pressure drop in N/m² due to the Bernoulli effect.

Apply the Bernoulli equation:

`P_1+\rho gh+(1)/(2)\rho v_1^2=P_2+\rho gh+(1)/(2)\rho v_2^2`

Thus, we have:

`P_1-P_2=(1)/(2)\rho(v_2^2-v_1^2)`

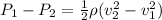
Apply the volumetric flow rate, where:

`v=(Q)/(A)`

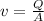
Thus, we have:

`P_1-P_2=(1)/(2)\rho((Q^2)/(A_2^2)-(Q^2)/(A_1^2))`

Solving further:

Where A is the area

`\begin{gathered} =(1)/(2)\rho Q^2((1)/(((\pi d_2^2)/(4))^2)-(1)/(((\pi d_1^2)/(4))^2)) \\ \\ =(1)/(2)(1000)(38*10^(-3))^2((1)/(((\pi *(9.20*10^(-2))^2)/(4))^2)-(1)/(((\pi *(3.10*10^(-2)))/(4))^2)) \\ \\ =−1.25*10^(-6)\text{ N/m}^2 \end{gathered}`

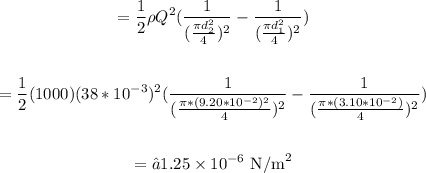
Therefore, the pressure drop is 1.25 x 10⁻⁶ N/m²

Part B).

To what maximum height (in m) above the nozzle can this water rise?

Also, apply the Bernoulli equation:

`P_1+\rho g(0)+(1)/(2)\rho v_1^2=P_1+\rho gh+(1)/(2)p(0)`

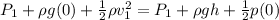
Thus, we have:

`(1)/(2)\rho v_1^2=\rho gh`

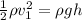
Where h is the height.

Rewrite the formula for h:

`\begin{gathered} h=(\rho v_1^2)/(2\rho g) \\ \\ h=(v_1^2)/(2\rho g) \\ \\ h=(Q^2)/(2gA_1^2)=(Q^2)/(2g((\pi d_1^2)/(4))^2) \\ \\ h=((38*10^(-3))^2)/(2*9.8*((\pi(3.1*10^(-2))^2)/(4))^2) \\ \\ h=129.33\text{ m} \end{gathered}`

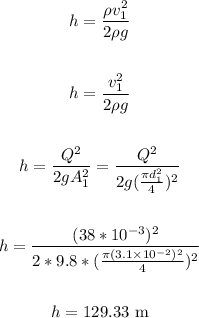
ANSWER:

a). 1251052.85 N/m²

(b). 129.33 m