A projectile motion is projected at an angle of 40°, at a height of 7 feet, and at an initial velocity of 20 ft/s.
It is required to find the parametric equations that represent the motion.
Recall that the Parametric Equations that represent a projectile motion with angle θ, initial velocity v_0, and height h is given as:
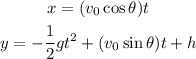
Where g=32 ft/s² is the acceleration due to gravity.
Substitute the constant g, the initial velocity, the height, and the angle of projection.
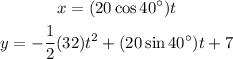
Simplify the equations and round final values to the nearest tenth:
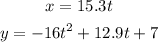
Hence, the required parametric equations.