Question

Sum of the first n terms of an arithmetic sequence

Answer 1

Given

`\begin{gathered} a)\text{ }-1+3+7+...+551 \\ b)\text{ }\sum_{i\mathop{=}1}^(79)(2i+6) \end{gathered}`

To find the sum of the arithmetic sequence.

Step-by-step explanation:

It is given that,

`\begin{gathered} a)\text{ }-1+3+7+...+551 \\ b)\text{ }\sum_{i\mathop{=}1}^(79)(2i+6) \end{gathered}`

That implies,

a) Here, the first term, the last t and common difference is,

`\begin{gathered} a=-1,d=3-(-1)=3+1=4,l=551 \\ \Rightarrow a=-1,d=4,l=551 \end{gathered}`

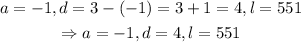
And,

`\begin{gathered} n=(l-a)/(d)+1 \\ =(551-(-1))/(4)+1 \\ =(552)/(4)+1 \\ =138+1 \\ =139 \end{gathered}`

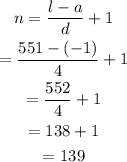
Then, the sum is given by,

`\begin{gathered} S_n=(n)/(2)(a+l) \\ =(139)/(2)(-1+551) \\ =(139)/(2)*550 \\ =139*275 \\ =38225 \end{gathered}`

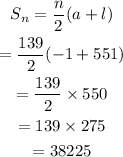
Hence, the sum is 38225.

Also,

b) It is given that,

`\sum_(i=1)^(79)(2i+6)=8,10,12,...,164`

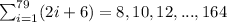
Here, the first term, common difference and the last term are,

`\begin{gathered} a=8,d=10-8=2,l=164 \\ a=8,d=2,l=164 \end{gathered}`

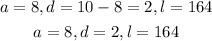
And,

`n=79`

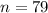
Then, the sum is given by,

`\begin{gathered} S_n=(n)/(2)(a+l) \\ S_(79)=(79)/(2)(8+164) \\ =(79)/(2)*172 \\ =79*86 \\ =6794 \end{gathered}`

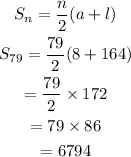
Hence, the sum is 6794.