Given: Triangles ABC and DEF are given such that
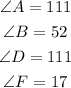
Required: To determine the similarity of the given triangles.
Explanation: Two triangles are said to be similar if their corresponding angles are equal.
In triangle ABC, we have-

Thus,
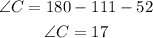
Now, in triangles ABC and DEF, we have

Therefore, by the AA rule of similarity
![\Delta ABC\approx\Delta DEF]()
Final Answer: Option C is correct.