Question

Mary's school is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 5 adults tickets and 2 student tickets for a total of $33. The school took in $39 on the second day by selling 1 adult ticket and 4 student tickets. How many student tickets did the school sell on the third day if the school sold 9 adult tickets and collected $117?

Answer 1

We can model the situation using a system of linear equations. Let a be the price of the adults' tickets and s the price that the students have to pay.

Then we have

`\begin{gathered} \text{first day} \\ 5a\text{ + 2s = 33} \\ \text{second day} \\ 1a+4s=39 \end{gathered}`

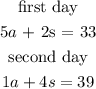
so we have two equaions. If we solve for a in the second equation and replace it on the first one we have

`\begin{gathered} a=39-4s \\ 5(39-4s)+2s=33 \\ 195-20s+2s=33 \\ 195-33=20s-2s \\ 18s\text{ = 162} \\ s=9. \end{gathered}`

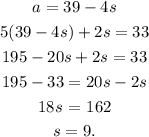
So the price of the tickets to the students is 9 dlls, and the price for the adult's ticket is

`a=39-4(9)=39-36=3`

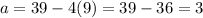
it's 3 dlls.

So, the last part says that, if we represent the numbers of tickets that were sold to the students by x, then

`\begin{gathered} 9(3)+9x=117 \\ 9x=117-27 \\ 9x=90 \\ x=10 \end{gathered}`

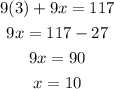
then, they sold 10 tickets to the students.