Given:
Distance from the sideline to the pole = 24 feet
Height of pole = 50 feet
Distance at which the light beam hits the soccer field = 37 feet from the sideline
The diagram beow represents this situation.
The figure above represents this situation.
From the figure, the angle a, represents the angle at which the lamp is set so that the light bem hits the socer field at 37 feet.
Let;s find the angle the lamp should be set (angle a).
To find the angle, apply trigonometric ratio formula for tan.
We have:
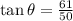
Take the inverse tangent of both sides:
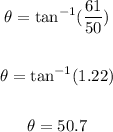
Therefore, the lamo should be set at an angle of 50.7 degrees to meet the stated conditions.
Let;s find the distance from the base of the pole to the where the center of the light hits the field.
New angle = 50.7 + 1 = 51.7 degrees
To find the distance, apply the trigonometric formula for tan:
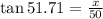
Multiply 50 to both sides:
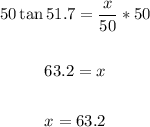
Therefore, if the angle increases by 1, the new distance from the bae of the pole to where the center of the light hits the field is 63.2 feet.
To find the increase in the distance, we have:
Increase = new distance - old distance
= 63.2 - 61 = 2.2 ft
Therefore, if the measure of the angle increases by 1, the distance from the base of the pole to the center where the light hits is 2.2 feet
ANSWER:
a. 51.7 degrees
b. 2.2 feet