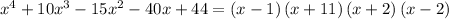Solution:
Given:
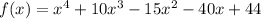
The zeros of the function are as follows;
Using the theorem, if f(a) = 0, then x = a is a root or zero.
Hence;
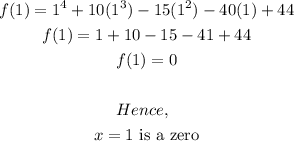
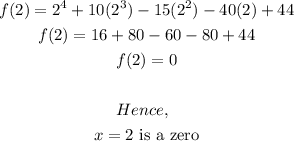
Trying other numbers, it follows also that;
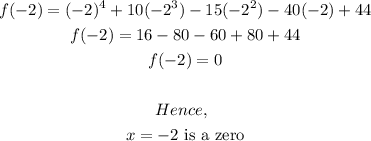
The last root is;
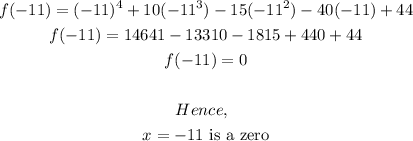
Therefore, the zeros are;
x = 1
x = 2
x = -2
x = -11
Using the factor theorem, if x = a is a zero, then (x-a) is a factor.
Thus,
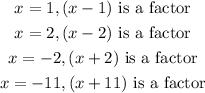
Hence, the polynomial can be factored as;