Since the given function is
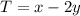
We will substitute each point in the equation, then find the smallest answer
For point (3, -2)
x = 3, y = -2
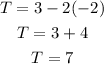
For point (-2, 3)
x = -2, y = 3
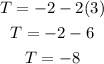
For point (-3, -2)
x = -3, y = -2
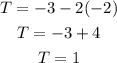
For the point (2, -3)
x = 2, y = -3
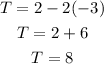
The minimum value is -8
Then the vertex is (-2, 3)
The answer is B