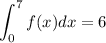Answer: 6
==============================================
Step-by-step explanation:
Split the graph into separate regions (see the diagram below)
The red trapezoid has the parallel vertical sides of b1 = 1 and b2 = 2. The height of the trapezoid is h = 2
The area of the red trapezoid is
A = h*(b1+b2)/2 = 2*(1+2)/2 = 3
--------------
The blue rectangle has a horizontal side of 2 and vertical side of 2. Its area is 2*2 = 4 square units.
--------------
The pink triangle has a base of 1 and height of 2
area = base*height/2 = 1*2/2 = 1 square unit
--------------
The green triangle has an area of base*height/2 = 2*2/2 = 2 square units
--------------
For any region above the x axis, it gets assigned a positive area. Anything below the x axis gets a negative area to counterbalance the positive areas.
The regions above the x axis add to 3+4+1 = 8 square units. Then we subtract off the area of the green triangle to get 8-2 = 6 square units.
Therefore,