Given data:
An empty swimming pool needs to be filled to the top. The pool is shaped like a cylinder with a diameter of 10m, and a depth of 1.7m.
The water is pumped into the pool at a rate of 12 meter cube per hour.
The formula for the volume of a cylinder is
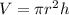
where,
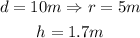
Thus,
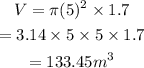
At a rate of 12 meter cube per hour.
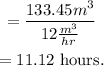
It will take 11.12 hours to fill the empty pool