Question

I’m trying to teach myself this…I just need a few answers to get me started! Thank you! I need all work shown please!! Was out for covid and teacher won’t help!

Answer 1

`\begin{gathered} y=8x-1000 \\ Profit=\$8 \\ Amount-Lost\Rightarrow\$1000 \end{gathered}`

Step-by-step explanation

We want to write a linear equation that represents the situation:

The general form of a linear equation is:

`y=mx+b`

where m = slope; b = y-intercept

Let the profit/loss be y.

Let the number of calendars sold be x.

After selling 80 calendars, they had a loss of $360. This implies that when x is 80, y is -$360:

`(x_1,y_1)=(80,-360)`

After selling 200 calendars, they had a profit of $600. This implies that when x is 200, y is $600:

`(x_2,y_2)=(200,600)`

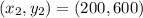
Now, we have two points that describe the relationship between profit/loss and the number of calendars sold.

To find the linear equation, we first have to find the slope using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Hence, the slope is:

`\begin{gathered} m=(600-(-360))/(200-80) \\ m=(600+360)/(200-80)=(960)/(120) \\ m=8 \end{gathered}`

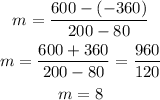
To find the equation that describes the relationship between profit/loss and the number of calendars sold, apply the point-slope method:

`y-y_1=m(x-x_1)`

Therefore, the equation is:

`\begin{gathered} y-(-360)=8(x-80) \\ y+360=8x-640 \\ y=8x-640-360 \\ y=8x-1000 \end{gathered}`

Since the slope represents the rate of the equation (i.e. the profit/loss per calendar sold), and the slope is positive, it implies that the profit made from selling each calendar is $8.

To find how much they would have lost if they sold no calendars, we have to find the value of the equation when x is 0. This is equivalent to the y-intercept of the equation.

Comparing the equation gotten to the general form of the linear equation, we see that the y-intercept of the equation is -$1000 (the negative indicates a loss).

This implies that they would have lost $1000 if they sold no calendars.