Question

Hello, I need help with the problem pictured. Thank you.

Answer 1

We have the following coordinates for the vertices of a quadrilateral:

• A = (1,1)

,

• B = (3,4)

,

• C = (8,3)

,

• D = (4,3)

We must perform the following transformation to the points:

0. A rotation of 180° about the origin.

,

1. A translation of 6 units up.

We make the rotation and then the translation.

1) We must note that the rule for a rotation by 180° about the origin is:

`X=(x,y)\rightarrow X^(\prime)=(-x,-y)`

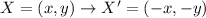
Making the rotation to the points, we get:

A' = (-1,-1)

B' = (-3,-4)

C' = (-8,-3)

D' = (-4,-3)

2) The translation of the points in 6 units up consists in making the following transformation:

`X^{}=(x,y)\rightarrow X^(\prime)=(x,y+6)`

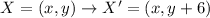
Making the translation, we get:

A'' = (-1,-1 + 6) = (-1,5)

B'' = (-3,-4 + 6) = (-3,2)

C'' = (-8,-3 + 6) = (-8,3)

D'' = (-4,-3 + 6) = (-4,3)

Answer

After making the two transformations to the points their coordinates are:

A'' = (-1,5)

B'' = (-3,2)

C'' = (-8,3)

D'' = (-4,3)