To answer this question, we need:
1. Find the area of the sector with a 90-degree angle.
2. Find the area of the triangle in the figure.
3. Subtract the area of the 90-degree angles minus the area of the triangle.
We can proceed as follows:
Area of the sector with a 90-degree angle
To find it, we can use the next formula:
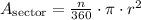
Where, in this case, n = 90 (number of degrees in central angle of the sector). We also have that r = 16 units (the radius of the circle). Now, we can calculate this area:
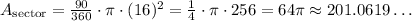
The area, in this case, is 64pi square units or 201.0619 square units.
Area of the triangle in the figure
Since this is a right triangle, we have that the base = 16 units, and the height is equal to 16 too. Then, we have:
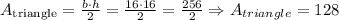
Now, we have that the area of the triangle is 128 square units.
Area of the Blue RegionThis area is:

Therefore, the area of the blue region is, approximately, equals to 73.0619 square units.