Question

K2CO3Percent composition of the following compounds

Answer 1

The percent composition is 56.6% of K, 8.7% of C and 34.7% of O.

1st) It is necessary to calculate the molar mass of K2CO3 from the atomic mass of each element:

- K atomic mass: 39.1 g/mol

- C atomic mass: 12 g/mol

- O atomic mass: 16 g/mol

K2CO3 molar mass = (K atomic mass).2 + C atomic mass + (O atomic mass).3

K2CO3 molar mass = (39.1 g/mol . 2) + 12 g/mol + (16 g/mol).3

K2CO3 molar mass = 138.2 g/mol

2nd) Now we can calculate the percentage composition of each element in the K2CO3 molecule since the 138.2g represents the 100% of the molecule:

Here it is important to consider the amount of each element in the K2CO3 molecule.

- Potassium (K):

In this calculation we have to consider that there are 2 moles of K, so the potassium total weigh is 78.2g (39.1gx2) in the molecule:

`\begin{gathered} 138.2g\text{ - 100\%} \\ 78.2g-x=\frac{78.2g\cdot\text{100\%}}{138.2g} \\ x=56.6\% \end{gathered}`

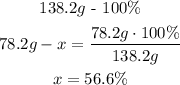
- Carbon (C):

Here we have to consider that there is only 1 mole of carbon, so the carbon total weigh is 12g in the molecule:

`\begin{gathered} 138.2g\text{ - 100\%} \\ 12g-x=\frac{12g\cdot\text{100\%}}{138.2g} \\ x=8.7\% \end{gathered}`

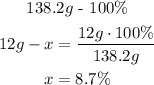
- Oxygen (O):

Here we have to consider that there are 3 mole of oxygen, so the oxygen total weigh is 48g (16gx3) in the molecule:

`\begin{gathered} 138.2g-100\% \\ 48g-x=(48g\cdot100\%)/(138.2g) \\ x=34.7\% \end{gathered}`

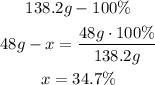
So, the percent composition is 56.6% of K, 8.7% of C and 34.7% of O.

Finally, to check that it is well resolved, we can add up all the percentages and verify that the total is equal to 100%:

56.6% + 8.7% + 34.7% = 100%