Answer:
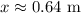
Explanation:
The weight of the airplane is hanging from the rubber band is represented by the multiplication between its mass (1.3 kg) and the acceleration due to gravity, which is 9.8 m/s^2.
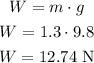
This situation can be modeled by Hook's law, which states that the force acting on a spring is given by:
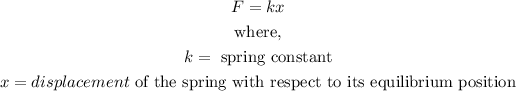
Substituting the given values, F=12.74 N and k=20 N/m.
Isolate x and solve:
