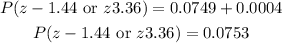Answer
0.0753
Explanation
First, we need to compute the z-scores of the situations.
z-score is calculated with the next formula:

where
• x: observed value
,
• μ: mean
,
• σ: standard deviation
Substituting μ = $580, σ = $125, x = $400, in one case, and x = $1000, in the other case, we get:
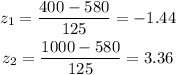
The probability a random person from Superior has less than $400 or more than $1000 in their bank account is calculated as follows:
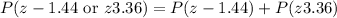
From the above table:
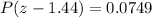
From the above table:
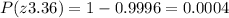
Substituting these results into the formula: