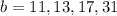We are given the following polynomial

We are asked to find the possible values of b that make the trinomial factorable.
The value of b must be such that
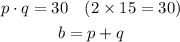
So what could be the two numbers so that their product will be 30?
How about 30 and 1?
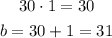
So, b = 31 is one of the possible values.
How about 15 and 2?
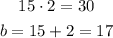
So, b = 17 is one of the possible values.
How about 10 and 3?
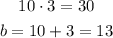
So, b = 13 is one of the possible values.
How about 6 and 5?
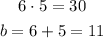
So, b = 11 is one of the possible values.
Therefore, all the possible values of b from least to greatest are