we have the equation
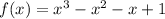
For x=1
f(x)=0
that means------> x=1 is a real root
Divide the given function by the factor (x-1)
x^3-x^2-x+1 : (x-1)
x^2-1
-x^3+x^2
-------------------
-x+1
x-1
---------
0
therefore
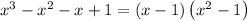
Solve the quadratic equation
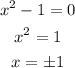
therefore
The equation has 3 real roots
Option C