Given:
Speed of sound, v = 344 m/s
Low frequency, fl = 30 Hz.
High frequency, fh = 25 kHz.
Let's find the audible range of sound spectrum.
The range of sound can be said to be the wavelength.
To find the wavelength, apply the formula:
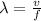
Where:
• λ is the wavelength in meters (m).
,
• v is the speed in meters per second (m/s)
,
• f is the frequency (Hz.)
• To find the largest wavelength, we have:
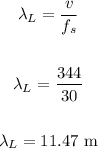
• To find the smallest wavelength, we have:
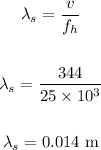
Therefore, we have:
Smallest value: 0.014 m
Largest value: 11.47 m
ANSWER:
• Smallest value: , 0.014 m
,
• Largest value: , 11.47 m