Question

A town has a population of 16000 and grows at 4.5% every year. What will be thepopulation after 8 years, to the nearest whole number?

Answer 1

Answer:

22752

Explanations:

Let the initial population be P

P = 16000

Let the annual growth rate be represented as r

r = 4.5%

let the time be represented as t

t = 8 years

Let the population after 8 years be represented as A

`A\text{ = }P(\text{ 1 + }r)^t`

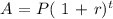
Substitute the values of P, r, and t into the equation above

`\begin{gathered} A\text{ = 16000(1 + }0.045)^8 \\ A=16000(1.045)^8 \\ A\text{ = }16000(1.422) \\ A\text{ = }22752 \end{gathered}`

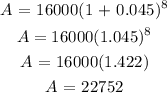
The population after 8 years is 22752