Answer:
Given function is,

To approximate the area under the curve in the interval [0, 20] by dividing the area into the given numbers of rectangles.
1) To use five rectangles to approximate the area under the curve.
we get that,
width of each rectangle is, (where a and b are end points of the interval)
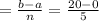
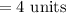
width of each rectangle is 4 units.
we get the x values as, 4,8,12,16 and 20
We can now calculate the height of each rectangle. So we figure the y-value of each corner of the rectangles. We get the following heights:
when x=4 we get,
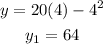
x=8 we get,

x=12 we get
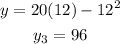
x=16 we get,
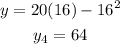
x=20 we get,
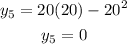
Area under the curve using 5 rectangle is,

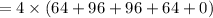
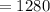
Area under the curve using 5 rectangle is 1280 sq.units.
Use 10 rectangles to approximate the area under the curve.
width of each rectangle is, (where a and b are end points of the interval)
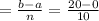

width of each rectangle is 2 units.
we get the x values as, 2,4,6,8,10,12,14,16,18 and 20
We can now calculate the height of each rectangle. So we figure the y-value of each corner of the rectangles. We get the following heights:
when x=2 we get,
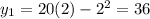
when x=4 we get,
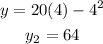
x=6 we get,
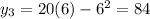
x=8 we get,
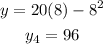
x=10 we get,

x=12 we get
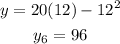
x=14 we get,

x=16 we get,
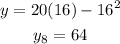
x=18 we get,
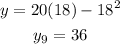
x=20 we get,
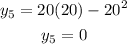
Area under the curve using 5 rectangle is,

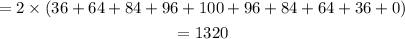
Area under the curve in the interval [0, 20] by dividing the area into 10 number of rectangles is 1320 sq units.