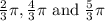Question

Finding solutions in an interval for a trigonometric equation in factored form

Answer 1

Given the trigonometry equation below

`(2\cos x+1)(2\sin x+\sqrt[]{3})=0`

If two numbers multiplies themselves and the result is zero, it implies that one of them is zero or both are zero

For instance:

`\begin{gathered} \text{If} \\ a* b=0 \\ a=0\text{ or }b=0 \end{gathered}`

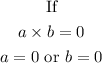
Thus,

`\begin{gathered} 2\cos x+1=0 \\ OR \\ 2\sin x+\sqrt[]{3}=0 \end{gathered}`
`\begin{gathered} 2\cos x+1=0 \\ \Rightarrow2\cos x=-1 \\ \Rightarrow(2\cos x)/(2)=(-1)/(2) \\ \therefore cosx=-(1)/(2) \\ x=\cos ^(-1)-(1)/(2) \\ \text{Values of x}\Rightarrow120^0,240^0 \\ In\text{ radian} \end{gathered}`
`\begin{gathered} 120^0*(\pi)/(180^0)=(2\pi)/(3)=(2)/(3)\pi \\ 240^0*(\pi)/(180^0)=(4\pi)/(3)=(4)/(3)\pi \end{gathered}`

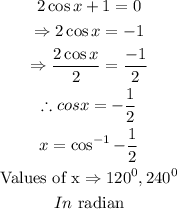
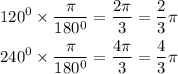
For

`\begin{gathered} 2\sin x+\sqrt[]{3}=0 \\ 2\sin x=-\sqrt[]{3} \\ \Rightarrow\sin x=-\frac{\sqrt[]{3}}{2} \\ x=\sin ^(-1)(-\frac{\sqrt[]{3}}{2}) \\ \therefore x\Rightarrow240^0,300^0 \end{gathered}`

In radian,

`\begin{gathered} 300^0*(\pi)/(180^0)=(5\pi)/(3)=(5)/(3)\pi \\ \end{gathered}`

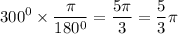
Hence, the solutions in radians of the equation in the interval [0, 2π) is

`(2)/(3)\pi,(4)/(3)\pi\text{ and }(5)/(3)\pi`