Question

A triangle has side lengths measuring 10m, 24m, and 26m. Explain how you use Pythagorean Theorem to determine whether or not the triangle is a right triangle.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about the pythagorean theorem and right triangles.

Given a triangle with side lengths 10 m, 24 m and 26 m, we have to determine whether this is a right triangle or not.

First, let's assume these are the sides lengths of a right triangle, as follows:

Notice in this case we choose the largest side to be the hypotenuse. We know that the largest side of a triangle has to be less than the sum of the legs and any combination would do, but since we'll apply the Pythagorean theorem, we already know that the hypotenuse has to be the largest side of the triangle.

For a right triangle with legs a, b and hypotenuse c, the Pythagorean theorem says that the sum of the squares of the legs is equal to the square of the hypotenuse, that is

`a^2+b^2=c^2`

Hence we plug a = 10, b = 24 and c = 26.

We have to see if this equality will hold for the values;

`10^2+24^2=26^2`

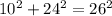
On the right hand side, square the number

`676`

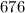
On the left hand side, square and add the numbers

`100+576=676`

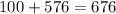
Notice we got the same answer, then we say that these values satisfy the Pythagorean theorem.

Therefore, this is a right triangle.