The question asks us to confirm the simplification of the expression:
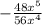
Step 1: Factor the numbers
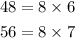
Therefore, the expression becomes:
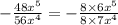
Step 2: Cancel out the common terms from the expression
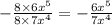
Step 3: Apply the rule of exponents
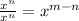
Therefore, we have:
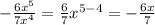
CONCLUSION
The expression simplifies to give:
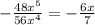
The answer is TRUE.