Question

`4 ^{ (1)/(3) } * 4 ^{ (1)/(5) } =`pls answer this

Answer 1

The given Expression is :

`4^{(1)/(3)}\cdot4^{(1)/(5)}`

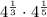
From the property of exponents

If the base value of the exponents are same then during the process of multiplication powers will add up.

Since in the given expression 4 is the base value on both base of the exponents

Thus, base value are equal

The powers will add up:

`\begin{gathered} 4^{(1)/(3)}\cdot4^{(1)/(5)} \\ 4^{(1)/(3)+(1)/(5)} \end{gathered}`

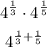
Simplify the farction of the exponents :

`\begin{gathered} (1)/(3)+(1)/(5) \\ \text{Taking LCM of the 3 \& 5} \\ (1)/(3)+(1)/(5)=(5+3)/(15) \\ (1)/(3)+(1)/(5)=(8)/(15) \end{gathered}`

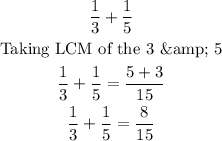
So, the value of the given expression will be :

`\begin{gathered} 4^{(1)/(3)}\cdot4^{(1)/(5)}=4^{(1)/(3)+(1)/(5)} \\ 4^{(1)/(3)}\cdot4^{(1)/(5)}=4^{(8)/(15)} \end{gathered}`

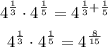
Answer : 4 ^8/15