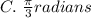Given the terminal point of Θ:
![((1)/(2),\frac{\sqrt[]{3}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/p18njdh7jvd6xsiojvhohqm1tk89o2nbgx.png)
Let's find the value of Θ.
In polar coordinates, we have the points as
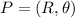
Where:
R is the radius and Θ is the angle.
We know in rectangular coordinates, we have:
x = R * cosΘ
Y = R * sinΘ
Thus, to find the value of Θ, we have:
![\sin \theta=\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/xlbqkc4ononzdmzcay8b9sgbke7osana1w.png)
Solve for Θ.
![\begin{gathered} \\ \text{sin}\theta=\frac{\sqrt[]{3}}{2} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o5m3k26qje0j8c5mgyu0qcnhdxx10r0ic7.png)
Take the inverse cosine of both sides:
![\begin{gathered} \theta=\sin ^(-1)(\frac{\sqrt[]{3}}{2}) \\ \\ \theta=(\pi)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/img4tziao854eliu03f9je7ky2y5k4llol.png)
ANSWER: