Question

A ball is thrown in the air from a platform that is 96 feet above ground level with an initial vertical velocity of 32 feet per second. The height of the ball, in feet, can be represented by the function shown where t is the time, in seconds, since the ball was thrown. Rewrite the function in the form that would be best used to identify the maximum height of the ball and find Approximately when the object lands on the ground when rounded to the nearest tenth.

Answer 1

y = -16 (x - 1)^2 + 112

The object lands on the ground in approximately 3.6s

Step-by-step explanation:

The equation given is that of a parabola.

Now the maximum (local) point of a parabola is the vertex. Therefore, if we want to rewrite our function in the form that would be used to find the maximum height, then that form must be the vertex form of a parabola.

The vertex form of a parabola is

`y=a(t-h)^2+k`

where (h, k) is the vertex.

The only question is, what is the vertex for our function h(t)?

Remember that if we have an equation of the form

`y=ax^2+bx+c`

then the x-coordinate of the vertex is

`h=-(b)/(2a)`

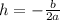
Now in our case b = 32 and a = -16; therefore,

`h=(-32)/(2(16))=1`

We've found the value of the x-coordinate of the vertex. What about the y-coordinate? To get the y-coordinate, we put x = 1 into h(t) and get

`k=-16(1)+32(1)+96=112`

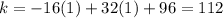
Hence, the y-coordindate is k = 112.

Therefore, the vertex of the parabola is (1, 112).

With the coordinates of the vertex in hand, we now write the equation of the parabola in vertex form.

`h(t)=a(t-1)^2+112`

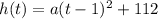
The only problem is that we don't know what the value of a is. How do we find a?

Note that the point (0, 96) lies on the parabola. In other words,

`h(0)=-16(0)^2+32(0)+96=96`

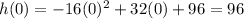
Therefore, the vertex form of the parabola must also contain the point (0, 96).

Putting in t = 0, h = 96 into the vertex form gives

`96=a(0-1)^2+112`
`96=a+112`

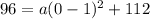
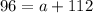
subtracting 112 from both sides gives

`a=-16`

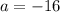
With the value of a in hand, we can finally write the equation of the parabola on vertex form.

`\boxed{h\mleft(t\mright)=-16\left(t-1\right)^2+112.}`

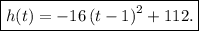
Now when does the object hit the ground? In other words, for what value of t is h(t) = 0? To find out we just have to solve the following for t.

`h(t)=0.`

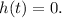
We could either use h(t) = -16t^2 + 32t + 96 or the h(t) = -16(t - 1)^2 + 112 for the above equation. But it turns out, the vertex form is more convenient.

Thus we solve,

`-16\left(t-1\right)^2+112=0`

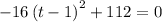
Now subtracting 112 from both sides gives

`-16(t-1)^2=-112`

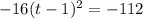
Dividing both sides by -16 gives

`(t-1)^2=(-112)/(-16)`
`(t-1)^2=7`

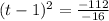
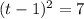
taking the square root of both sides gives

`t-1=\pm√(7)`

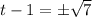
adding 1 to both sides gives

`t=\pm√(7)+1`

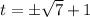
Hence, the two solutions we get are

`t=√(7)+1=3.6`
`t=-√(7)+1=-1.6`

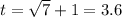
Now since time cannot take a negative value, we discard the second solution and say that t = 3.6 is our valid solution.

Therefore, it takes about 3.6 seconds for the object to hit the ground.