Question

“A falcata is formed by taking a quadrant of a circle and removing a semicircle from it (see diagram).If the radius of the original circle is 2 units long, find the exact area of the falcata.”hello!! please help me out! i’m begging. this assignment is kicking my teeth in!!

Answer 1

step 1

Find out the area of the complete quadrant of the circle (1/4 of the complete circle)

`A=(1)/(4)*pi*r^2`

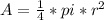
where

r=2 units

substitute

`\begin{gathered} A=(1)/(4)*pi*2^2 \\ A=pi\text{ unit}^2 \end{gathered}`

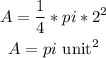
step 2

Find out the area of the semicircle removed

`A=(1)/(2)*pi*r^2`

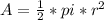
where the radius of the semicircle removed is half of the radius of the circle

so

r=2/2=1 unit

`\begin{gathered} A=(1)/(2)*pi*1^2 \\ A=(pi)/(2)\text{ unit}^2 \end{gathered}`

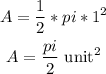
therefore

to find out the area of the falcata, subtract the area of the removed semicircle from the area of the quadrant of the circle

The area of the falcata is

A=pi-pi/2=pi/2 unit2

the area of the falcata is pi/2 square units