Question

Given z1 = 5(cos 240° + isin 240°) and z2 = 15(cos 135° + isin 135°), what is the product of z1 and z2?

Answer 1

By multiplying z1 and z2, we get:

`\begin{gathered} z1* z2=5(cos240+isin240)15(cos135+isin135) \\ z1* z2=75(cos240+isin240)(cos135+isin135) \end{gathered}`

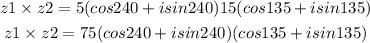
Applying the distributive property:

`\begin{gathered} z1* z2=75(cos240+\imaginaryI s\imaginaryI n240)(cos135+\imaginaryI s\imaginaryI n135) \\ z1* z2=75(cos240* cos135+cos240* isin135+\mathrm{i}s\mathrm{i}n240* cos135+\imaginaryI s\imaginaryI n240*\imaginaryI s\imaginaryI n135) \\ z*1z*2=75(cos240* cos135+cos240*\imaginaryI s\imaginaryI n135+\imaginaryI s\imaginaryI n240* cos135-s\imaginaryI n240* s\imaginaryI n135) \end{gathered}`

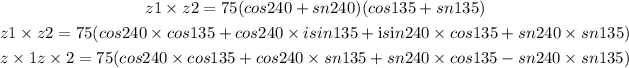
In order to simplify this, we can use the following trigonometric identities:

`\begin{gathered} sin(\alpha+\beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta) \\ cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta) \end{gathered}`

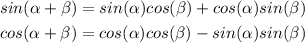
By taking β as 135 and α as 240, we can write:

`\begin{gathered} is\imaginaryI n(240+135)=isin(375)=is\imaginaryI n(240)s\imaginaryI n(135)+icos(240)s\imaginaryI n(135) \\ cos(240+135)=cos(375)=cos(240)cos(135)-s\imaginaryI n(240)s\imaginaryI n(135) \end{gathered}`

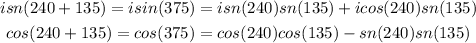
Then, by grouping some terms of the expression, we get:

`z*1z*2=75(cos(375)+isin(375))`

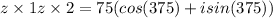
375° is equivalent to 15° (375 - 360 = 15), then the product of z1 and z2 can be finally written as:

`z1* z2=75(cos(15)+\imaginaryI s\imaginaryI n(15))`

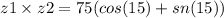
Then, option A is the correct answer