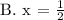Given the equation:
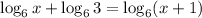
Let's solve for x.
To find the solution, take the following steps:
Step 1:
Apply the product property of logarithm to the left side of the equation:
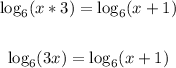
Step 2:
Eliminate the log on both sides
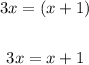
Step 3:
Subtract x from both sides
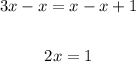
Step 4:
Divide both sides by 2
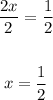
Therefore, the solution to the given equation is:
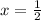
ANSWER: