Question

A population doubles every 27 years. Assuming exponential growth find the following:help find continuous growth rate (a) The annual growth rate: 2.6(b) The continuous growth rate is____% per year help (numbers)

Answer 1

Given,

A population doubles every 27 years.

a. Let initial population be 1 and after 27 years it becomes 2.

Considering r as the rate of annuall growth we have,

`\begin{gathered} 1(1+r)^(27)=2 \\ \Rightarrow27\ln (1+r)=\ln 2 \\ \Rightarrow\ln (1+r_{})=(0.693)/(27) \\ \Rightarrow1+r=1.0257 \\ \Rightarrow r=0.026 \end{gathered}`

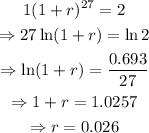
Thus annual growth rate is 2.6%

b. For continuous growth,

`\begin{gathered} 1(e^(27x))=2 \\ \Rightarrow27x=0.693 \\ \Rightarrow x=0.025 \end{gathered}`

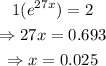
The continuous growth rate is _2.5___% per year