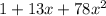ANSWER
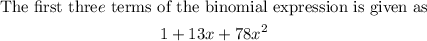
Explanation:
Given the following function
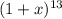
The above expression is a binomial expression
To find the first three terms, we need to apply the binomial theorem
The general formula for binomial theorem is given below as
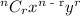
Let x = 1 and y = x
n = 13
r ranges from zero to 13

Hence, the first three terms of the binomial expression are given below as