In the question, we are given the following information about the production cost of the two methods.
For method 1, the one-time fixed costs will total $22,256, and the variable costs will be $25 per book.
For method 2, the one-time fixed costs will total $80,768, and the variable costs will be $11.75 per book.
This is a case of partial variation and we can derive two equations for the different production methods using the formula below.
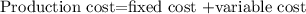
Let each book represents b
Thus;

To find the number of books produced that would make the costs from the two methods be the same, we would equate the equations above;
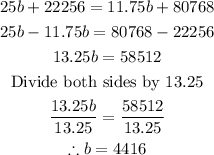
Therefore, the number of books produced that would make the costs from the two methods be the same is;
Answer: 4416