Question

17. If you borrow $150,000, how much could you save over the life of the loan if you took out a 20-year mortgage at 3.9% instead of a 30-year mortgage at 3.4%?

Answer 1

Let us calculate the monthly mortgage payment and the total payment for each condition given.

Please note that the formula for calculating monthly mortgage payment and Total payment is as shown below:

`\begin{gathered} M=P((r)/(12)(1+(r)/(12))^n)/((1+(r)/(12))^n-1) \\ TP=M* n \end{gathered}`

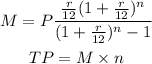
When the rate is 4% for 15 years, M and P is calculated as shown below:

`r=(4)/(100)=0.04,n=15*12=180`
`\begin{gathered} M=250,000(((0.04)/(12)(1+(0.04)/(12))^(180))/((1+(0.04)/(12))^(180)-1) \\ M=250,000((0.00333(1+0.00333)^(180))/((1+0.00333)^(180)-1) \\ M=250,000((0.00333(1.00333)^(180))/((1.00333)^(180)-1) \\ M=250,000((0.00333(1.820301627))/(1.820301627-1) \\ M=250,000((0.0060676114))/(0.820301627) \\ M=250,000(0.0073968) \\ M=1849.2 \end{gathered}`
`\begin{gathered} TP=M* n \\ TP=1849.2*180 \\ TP=332,856 \end{gathered}`

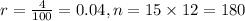
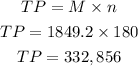
When the rate is 3.5% for 30 years, M and P is calculated as shown below:

`\begin{gathered} P=250,000,n=30*12=360,r=(3.5)/(100)=0.035 \\ M=250,000(((0.035)/(12)(1+(0.035)/(12))^(360))/((1+(0.035)/(12))^(360)-1) \\ M=250,000((0.0029167(1+0.0029167)^(360))/((1+0.0029167)^(360)-1) \\ M=250,000((0.0029167(1.0029167)^(360))/((1.0029167)^(360)-1) \\ M=250,000((0.0029167(2.853287165))/((2.853287165)-1) \\ M=250,000((0.008322087565))/(1.853287165) \\ M=250,000(0.004490446879) \\ M=1122.61 \end{gathered}`
`\begin{gathered} TP=M* n \\ TP=1122.61172*360 \\ TP=404,140.2191 \\ TP=404,140.22 \end{gathered}`

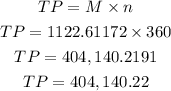
The amount that could be saved is subtracting the less total payment from the higher as shown below:

`\begin{gathered} \text{Amount saved } \\ =404,140.2191-332,856 \\ =71284.2191 \\ =71,284.22 \end{gathered}`

Hence, the amount would be saved is $71,284.22