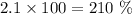Question

Compute the scale factor, as a percent, for each given relationship. When necessary, round your answer to the nearest tenth of a percent. 2 1.60 In 3.36 in a. Drawing 1 to Drawing 2 Drawing 2 to Drawing 1 Blank 1: Blank

Answer 1

`\begin{gathered} (a)\rightarrow(S_1)/(S_2)=0.48\rightarrow48\text{ \%} \\ \\ (b)\rightarrow(S_2)/(S_1)=2.1\rightarrow210\text{ \%} \end{gathered}`

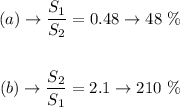
Step-by-step explanation: We are given two figures that are essentially similar, but one is scaled up, we need to find out the scale factor.

Two same given sides are:

`\begin{gathered} S_1=1.60in \\ S_2=3.36in \end{gathered}`

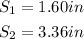
(a) Drawing 1 to Drawing 2:

`(S_1)/(S_2)=(1.60)/(3.36)\approx0.48`

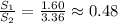
In percent would be:

`0.48*100=48\text{ \%}`

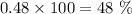
(b) Drawing 2 to Drawing 1:

`(S_2)/(S_1)=(3.36)/(1.60)=2.1`

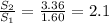
In Percent would be:

`2.1*100=210\text{ \%}`