Given: A geometric sequence with first term and the common ratio a1 = 5 and r = -3.
Required: Fifth term of the geometric series.
Step-by-step explanation:
In a geometric sequence, with first term 'a' and common ratio 'r'
nth term is

So the fifth term is
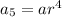
a = 5 and r = - 3.
So
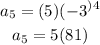
So
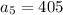
Final Answer: The fifth term of Geometric sequence is 405.