Question

Find the solution(s) of the system of equations.y = x² + 4xy + x² = –4xQuestion 20 options:A) (0, 0) and (4, 0)B) (–4, 0) and (4, 0)C) (0, 0)D) (–4, 0) and (0, 0)

Answer 1

(D) (–4, 0) and (0, 0)

Explanation:

Given the system of equations:

`\begin{gathered} y=x^2+4x| \\ y+x^2=-4x \end{gathered}`

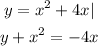
To solve, the substitution method is employed.

Substitute the first equation into the second equation.

`\begin{gathered} y+x^2=-4x \\ (x^2+4x)+x^2=-4x \\ \text{Collect like terms} \\ x^2+x^2+4x+4x=0 \\ 2x^2+8x=0 \\ \text{Factorize} \\ 2x\mleft(x+4\mright)=0 \\ 2x=0\text{ or }x+4=0 \\ x=0\text{ or }x=-4 \end{gathered}`

Next, find the values of y for each value of x using the first equation. (You can use any of the equations).

`\begin{gathered} y=x^2+4x \\ \text{When }x=0,y=0^2+4(0)=0\implies(0,0) \\ \text{When }x=-4,y=(-4)^2+4(-4)=16-16\implies(-4,0) \end{gathered}`

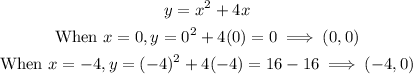
The solutions to the system of equations are (0,0) and (-4,0).

Option D is correct.