Question

Find the change in gravitational potential energy of the following a) A box of mass 10kg which is raised 1.6 meters vertically

Answer 1

We are asked to determine the change in gravitational potential energy. To do that we will use the following formula:

`\Delta U=mg\Delta h`

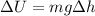
Where:

`\begin{gathered} \Delta U=\text{ change in potential energy} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ \Delta h=\text{ change in height} \end{gathered}`

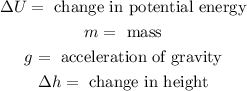
The change in height is the distance that the object is raised. Therefore, plugging in the values we get:

`\Delta U=(10kg)(9.8(m)/(s^2))(1.6m)`

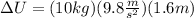
Solving the operations:

`\Delta U=156.8J`

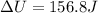
Therefore, the change in gravitational potential energy is 156.8 Joules.