Question

Question 12 please help. Find the number of solutions to the Quadratic Equation.

Answer 1

Given the Quadratic Equation:

`x^2=-7x+7`

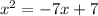
You need to rewrite it in this form:

`ax^2+bx+c=0`

Then, you need to move the terms on the right side to the left side (remember to change their signs):

`x^2+7x-7=0`

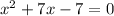
Now you can identify that:

`\begin{gathered} a=1 \\ b=7 \\ b=-7 \end{gathered}`

In order to find the type of roots or solutions the Quadratic Equation has, you can find the Discriminant using this formula:

`D=b^2-4ac`

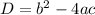
By substituting values into the formula and evaluating, you get:

`D=(7)^2-(4)(1)(-7)=77`

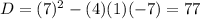
By definition, if:

`D>0`

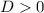
The Quadratic Equation has two different Real Roots.

Hence, the answer is: Option c.