The equation of a line in slope-intercept form looks like this:

Where m is the slope and b is the y-intercept. Any point that is part of this line must be a solution wo this equation. Looking at the picture you can see that the line passes through points (-5,1) and (0,-3). Then if we replace x and y in the former equation with the first and second coordinate of each of these points we'll have two equations:
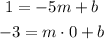
By solving these equations we find m and b which means that we'll find the equation requested. First is important to note that the second equation tells us the value of b:
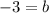
If we substitute this value in the first equation we get:
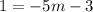
Now let's add 3 to both sides of this equation:
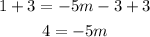
And we divide both sides by -5:
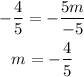
Now that we have both m and b we have the equation in slope-intercept form:

Which means that the answer is option A.