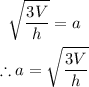Question

The formula for the volume of a right square pyramid is given below, where a is the side length of the base and h is the height.V = 1/3 (a^2)hRewrite the formula by solving for a.

Answer 1

`\begin{equation*} a=\sqrt{(3V)/(h)} \end{equation*}`

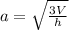
Step-by-step explanation:

Given:

`V=(1)/(3)a^2h`

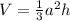
To:

Rewrite the formula by solving for a

We'll go ahead and make "a" the subject of formula by following the below steps;

Step 1: Cross multiply;

`3V=a^2h`

Step 2: Divide both sides by h;

`\begin{gathered} (3V)/(h)=(a^2h)/(h) \\ (3V)/(h)=a^2 \end{gathered}`

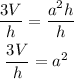
Step 3: Take the square root of both sides;

`\begin{gathered} \sqrt{(3V)/(h)}=a \\ \therefore a=\sqrt{(3V)/(h)} \end{gathered}`