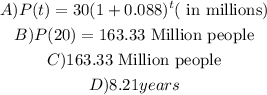
Step-by-step explanation
you can model growth by a constant percent increase with the following formula:

so
Step 1
make the model.
A)Let
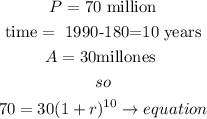
now, we need to solve for r

c) now, we can complete the model
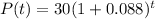
Step 2
Whar population do you predict for the year 2000?
Let
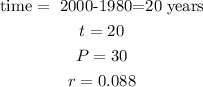
replace
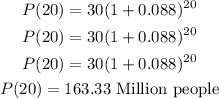
Step 3
D) What is the doubling time?
Doubling time =____ years
to solve this , we need to find the time , when population is double than currently, so
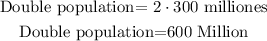
then, let
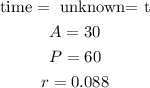
replace
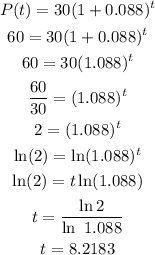
therefore, the time is
D)8.21 years
I hope this helps you