First, we analyze the relations given by the tangent function and the cosine function. We know that the tangent function is equal to the ratio between the opposite leg and the adjacent leg that means the opposite leg is 4 and the adjacent leg is 3.
Let's solve each expression.
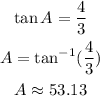

Then, we use these values to find cos (A+B).
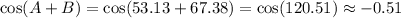
Hence, the answer is -0.51, approximately.