Question

a) Determine the equation of a cubic function passing through +1 and touching -2.b) Write an equation for the family member whose graph passes through the point (0, -12).

Answer 1

ANSWERS

(a) y = a(x - 1)(x + 2)²

(b) y = 3(x - 1)(x + 2)²

Step-by-step explanation

(a) If the graph of a cubic function touches (but does not pass through) a point on the x-axis, then that value of x is a double zero, represented by the square of the factor with that zero.

In this case, we have that one zero is +1, so one factor is (x - 1). The other factor is given by the double zero at x = -2, so the factor for that zero is (x + 2)².

Hence, the equation for the cubic function described is y = a(x - 1)(x + 2)²

The coefficient a is given to represent all the cubic functions that have a similar shape - i.e. have the same zeros with the same multiplicity.

(b) In this part, we have to find what is the value of the coefficient that makes the function pass through (0, -12). To find it, we have to replace x with 0 and y with -12 in the equation from part a,

`-12=a(0-1)(0+2)^2`

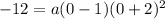
And solve for a. First, solve the additions in the parenthesis,

`-12=a(-1)(2)^2`

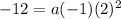
Solve the exponent,

`-12=a(-1)\cdot4`

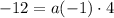
And the product,

`-12=-4a`

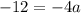
Finally, divide both sides by -4,

`\begin{gathered} (-12)/(-4)=(-4a)/(-4) \\ 3=a \end{gathered}`

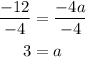
Hence, the equation for this family member is y = 3(x - 1)(x + 2)².